Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
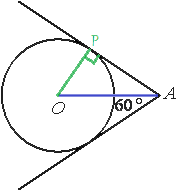Проведем отрезок АО.
Обозначим одну из точек касания окружности и касательной как Р.
Проведем отрезок ОР.
ОР является радиусом и перпендикуляром к касательной АР (по свойству касательной).
Рассмотрим треугольник АОР. Данный треугольник является прямоугольным,т.к. ОР перпендикулярен АР. АО является биссектрисой угла, образованного касательными (свойство касательных прямых).
Следовательно, угол РАО равен половине данного угла, т.е. 30°.
sin∠PAO=sin∠30°=1/2 (табличное значение).
Так же sin∠PAO=ОР/АО (по определению синуса).
sin∠30°=1/2=ОР/АО
AO=2*ОР=2*8=16.
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
Касательные в точках A и B к окружности с центром O пересекаются под углом 28°. Найдите угол ABO. Ответ дайте в градусах.
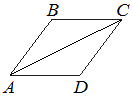В треугольнике ABC проведена биссектриса AL, угол ALC равен 52°, угол ABC равен 13°. Найдите угол ACB. Ответ дайте в градусах.
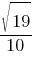Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=17 и MB=19. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: