
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.
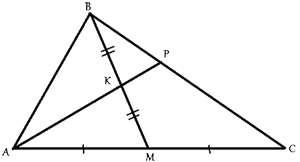 По условию задачи ВМ -
медиана треугольника АВС, следовательно, по
свойству медианы,
площади треугольников АВМ и ВСМ равны, и равны половине площади треугольника АВС.
По условию задачи ВМ -
медиана треугольника АВС, следовательно, по
свойству медианы,
площади треугольников АВМ и ВСМ равны, и равны половине площади треугольника АВС.
SABM=SBCM=(SABC)/2.
В свою очередь, AK является медианой для треугольника АВМ, следовательно, по тому же
свойству медианы
SABК=SAKM=(SABM)/2=(SABC)/4.
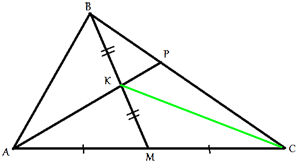 Проведем отрезок СК.
СК является
медианой для треугольника СМВ, следовательно,
Проведем отрезок СК.
СК является
медианой для треугольника СМВ, следовательно,
SCMK=SCKB=(SCMB)/2=(SABC)/4.
Проведем отрезок МЕ, параллельно АР.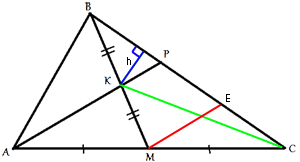 МЕ является
средней линией для треугольника АРС, следовательно (по
теореме о средней линии) СЕ=ЕР. А для треугольника МВЕ
КР является
средней линией, следовательно ВР=ЕР(=СЕ). Т.е. сторона ВС делится на три равные части точками
Р и Е.
МЕ является
средней линией для треугольника АРС, следовательно (по
теореме о средней линии) СЕ=ЕР. А для треугольника МВЕ
КР является
средней линией, следовательно ВР=ЕР(=СЕ). Т.е. сторона ВС делится на три равные части точками
Р и Е.
Проведем
высоту h, как показано на рисунке. h является общей высотой для треугольников СКВ и СКР.
Выше мы определили, что SCKB=(SABC)/4. Площадь этого же треугольника =(1/2)*h*BC.
SCKP=(1/2)*h*РС=(1/2)*h*(2/3)*ВС=(2/3)*(1/2)*h*BC=(2/3)SCKB=(2/12)SABC
=(1/6)SABC.
SKPCM=SCMK+SCKP=(SABC)/4+(1/6)SABC=(5/12)SABC.
SABC/SKPCM=12/5.
Ответ: SABC/SKPCM=12/5=2,4.
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.
В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.
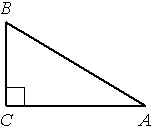 В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
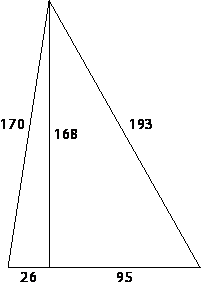 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
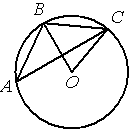 Точка О – центр окружности, /BAC=20° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=20° (см. рисунок). Найдите величину угла BOC (в градусах).
 Прямая, параллельная стороне
AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.
Прямая, параллельная стороне
AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.
Комментарии: