
 Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 48, а площадь равна 288.
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 48, а площадь равна 288.
Решение прислал пользователь Людмила
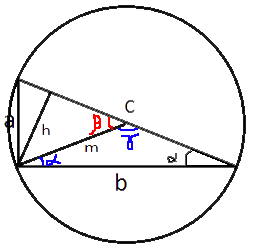 Проведем из прямого угла медиану и высоту, обозначив их m и h соответственно.
Проведем из прямого угла медиану и высоту, обозначив их m и h соответственно.
Если описать окружность вокруг треугольника, то центр этой окружности будет лежать на середине гипотенузы (по
теореме об описанной окружности). Следовательно:
m=c/2=48/2=24
S=(1/2)hc
h=2S/c=2*288/48=288/24=12
По
определению синуса:
sinβ=h/m=12/24=0,5
По таблице определяем, что β=30°
Угол γ является внешнем к β, следовательно γ=180°-β=180°-30°=150°
Треугольник, содержащий угол γ,
равнобедренный, так как медиана m и половина гипотенузы равны (это мы выяснили ранее).
Следовательно, по
свойству равнобедренного треугольника углы при основании равны (обозначены α).
Тогда, по
теореме о сумме углов треугольника:
180°=γ+α+α
180°=150°+2α
α=15° - это один из искомых углов.
Другой искомый угол найдем по той же
теореме об углах треугольника: 180°-90°-15°=75°
ответ: 15° и 75°
Поделитесь решением
Присоединяйтесь к нам...
 Радиус вписанной в квадрат окружности равен 2√2. Найдите диагональ этого квадрата.
Радиус вписанной в квадрат окружности равен 2√2. Найдите диагональ этого квадрата.
 Сторона AC треугольника ABC проходит через центр окружности. Найдите ∠C, если ∠A=30°. Ответ дайте в градусах.
Сторона AC треугольника ABC проходит через центр окружности. Найдите ∠C, если ∠A=30°. Ответ дайте в градусах.
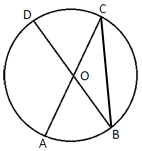 В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 128°. Найдите вписанный угол ACB. Ответ дайте в градусах.
В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 128°. Найдите вписанный угол ACB. Ответ дайте в градусах.
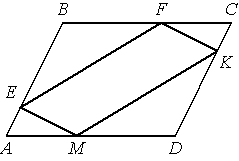 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
 В треугольнике ABC угол C прямой, AC=6, cosA=0,6. Найдите AB.
В треугольнике ABC угол C прямой, AC=6, cosA=0,6. Найдите AB.
Комментарии: