В трапеции ABCD основания AD и BC равны соответственно 33 и 11,
а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
Продлим стороны AB и CD до пересечения друг с другом.
Рассмотрим треугольник AED.
По
теореме о сумме углов треугольника:
180°=∠EDA+∠DAE+∠AED
180°=90°+∠AED
∠AED=90°
Следовательно треугольник AED -
прямоугольный.
Рассмотрим треугольники AED и BEC.
∠AED - общий
∠EBC=∠EAD (т.к. это
соответственные углы)
Треугольники AED и BEC
подобны (по
первому признаку подобия треугольников).
Тогда по
определению подобия:
AD/BC=AE/BE
AD/BC=(AB+BE)/BE
33/11=(20+BE)/BE
3=(20+BE)/BE
3BE=20+BE
2BE=20
BE=10
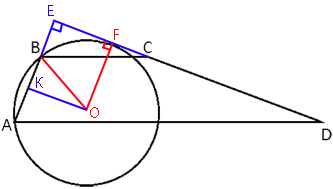Точка F - точка касания прямой CD и окружности.
По
теореме о касательной и секущей:
EF2=BE*AE=BE*(AB+BE)=10(20+10)=300
EF=√
Рассмотрим треугольник EOK.
О - центр окружности
OB - радиус окружности
OK -
серединный перпендикуляр к
хорде AB (
третье свойство хорды)
OK=EF (т.к. KEFO -
прямоугольник)
KB=AB/2 (т.к. OK -
серединный перпендикуляр)
По
теореме Пифагора:
OB2=OK2+KB2
OB2=(√
OB2=300+100=400
OB=20=R
Ответ: 20
Поделитесь решением
Присоединяйтесь к нам...
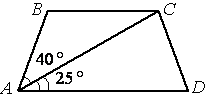Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
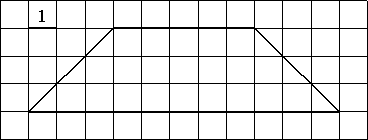Найдите площадь трапеции, изображённой на рисунке.
В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 170 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 340 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Прямая, параллельная стороне
AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:7, KM=12.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: