
 Основания BC и AD трапеции ABCD равны соответственно 5 и 45, BD=15. Докажите, что треугольники CBD и BDA подобны.
Основания BC и AD трапеции ABCD равны соответственно 5 и 45, BD=15. Докажите, что треугольники CBD и BDA подобны.
ABCD -
трапеция, следовательно, AD||BC.
∠CBD=∠ADB (т.к. это
накрест-лежащие углы для параллельных прямых AD и BC).
Рассмотрим отношения сторон:
BC/BD=5/15=1/3
BD/AD=15/45=1/3
Тогда по
второму признаку подобия треугольников, треугольники CBD и ADB подобны.
Поделитесь решением
Присоединяйтесь к нам...
Синус острого угла A треугольника ABC равен 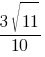 . Найдите CosA.
. Найдите CosA.
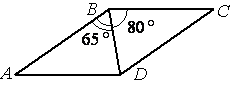 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма.
 Сторона ромба равна 38, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Сторона ромба равна 38, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
 Центральный угол AOB опирается на хорду АВ длиной 6. При этом угол ОАВ равен 60°. Найдите радиус окружности.
Центральный угол AOB опирается на хорду АВ длиной 6. При этом угол ОАВ равен 60°. Найдите радиус окружности.
 В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
Комментарии: