В треугольнике ABC угол C равен 90°, BC=6, sinA=0,6. Найдите AB.

Другие задачи из этого раздела

Задача №3B3D55

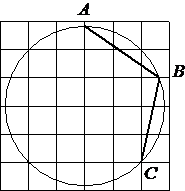Найдите угол ABC . Ответ дайте в градусах.

Задача №2D8927

Катеты прямоугольного треугольника равны 3√51 и 21. Найдите синус наименьшего угла этого треугольника.

Задача №0E2331

На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=32, MD=8, H — точка пересечения высот треугольника ABC. Найдите AH.

Задача №4081C6

Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 6 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.

Задача №061DDF

На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=27, MD=18, H — точка пересечения высот треугольника ABC. Найдите AH.