Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
Рассмотрим треугольник АОВ.
АО=ОВ, т.к. это радиусы окружности.
Следовательно, треугольник АОВ - равнобедренный.
Это значит, что ∠ОВА = ∠ОАВ = 60° (по свойству равнобедренного треугольника). Заметим, что ∠АОВ тоже равен 60° (по теореме о сумме углов треугольника). 180°-60°-60°=60°.
Следовательно, треугольник АОВ - равносторонний (по свойству равностороннего треугольника).
Получается, что ОВ=ОА=АВ=8.
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
Косинус острого угла A треугольника ABC равен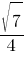 
. Найдите sinA.
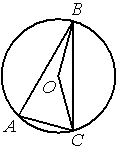Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
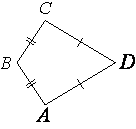В выпуклом четырехугольнике ABCD известно, что AB=BC, AD=CD, ∠B=133°, ∠D=173°. Найдите
угол A. Ответ дайте в градусах.
Найдите площадь трапеции, изображённой на рисунке.
В трапеции ABCD AB=CD, ∠BDA=67° и ∠BDC=28°. Найдите угол ABD. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: