
 Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 20, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 20, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
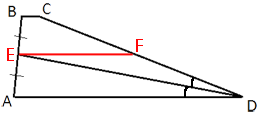 Проведем отрезок, параллельный основаниям, как показано на рисунке.
Проведем отрезок, параллельный основаниям, как показано на рисунке.
EF -
средняя линия трапеции, так как соединяет середины боковых сторон трапеции (по
теореме Фалеса).
∠ADE=∠DEF (так как это
накрест-лежащие углы при параллельных прямых EF и AD и секущей ED).
Получается, что ∠DEF=∠EDF (так как DE -
биссектриса).
Значит треугольник EFD -
равнобедренный (по
свойству равнобедренного треугольника).
Следовательно, EF=FD (по
определению).
EF=FD=CD/2=20/2=10
EF=(BC+AD)/2=10
(2+AD)/2=10
2+AD=20
AD=18
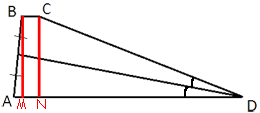 Проведем
высоты как показано на рисунке.
Проведем
высоты как показано на рисунке.
MN=BC=3 (т.к. BCNM -
прямоугольник).
BM=CN=h
Обозначим AM как x, для удобства.
AD=AM+MN+ND
18=x+2+ND
ND=16-x
Для треугольника ABM запишем
теорему Пифагора:
AB2=h2+x2
122=h2+x2
h2=144-x2
Для треугольника CDN запишем
теорему Пифагора:
CD2=h2+ND2
202=h2+(16-x)2
400=h2+(16-x)2
Подставляем вместо h2 значение из первого уравнения:
400=144-x2+(16-x)2
400-144=-x2+162-2*16*x+x2
256=162-2*16*x |:16
16=16-2x
2x=0
x=0, получается, что BM совпадает со стороной AB, т.е. AB является высотой трапеции.
Тогда площадь трапеции равна:
S=AB(AD+BC)/2=12(18+2)/2=6*20=120
Ответ: 120
Поделитесь решением
Присоединяйтесь к нам...
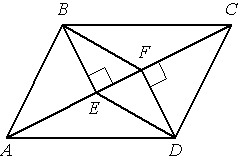 В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ — параллелограмм.
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ — параллелограмм.
 Радиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции.
Радиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции.
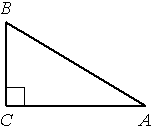 В треугольнике ABC угол C прямой, BC=9, sinA=0,3. Найдите AB.
В треугольнике ABC угол C прямой, BC=9, sinA=0,3. Найдите AB.
 Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 30 см, а длина – 40 см. Найдите расстояние между точками A и B (в метрах).
Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 30 см, а длина – 40 см. Найдите расстояние между точками A и B (в метрах).
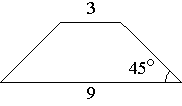 В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Комментарии: