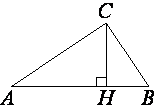
В прямоугольном треугольнике ABC катет AC=25, а высота CH, опущенная на гипотенузу, равна 10√
Вариант №1
Рассмотрим треугольники ABC и ACH.
∠AHC=∠ACB (т.к. это прямые углы).
∠A - общий.
Следовательно, по
теореме о сумме углов треугольника ∠ACH=∠ABC
Тогда sin∠ACH=sin∠ABC.
Теперь рассмотрим треугольник ACH.
По
теореме Пифагора:
AC2=CH2+AH2
252=(10√
625=100*6+AH2
AH2=625-600
AH2=25
AH=5
sin∠ACH=AH/AC (по
определению)
sin∠ACH=5/25=0,2
Как было выведено выше:
sin∠ABC=sin∠ACH=0,2
Ответ: sin∠ABC=0,2
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, sinA=0,75, AC=√
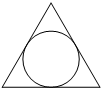Радиус окружности, вписанной в равносторонний треугольник, равен 10√3. Найдите длину стороны этого треугольника.
Радиус вписанной в квадрат окружности равен 2√2. Найдите радиус окружности, описанной около этого квадрата.
Стороны AC, AB, BC треугольника ABC равны 3√
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: