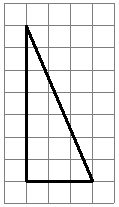
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Из
определения прямоугольного треугольника понятно, что катеты - это стороны прилегающие к прямому углу. В данной задаче катеты равны 7 и 3.
Очевидно, что 7 - длина большего катета.
Ответ: 7
Поделитесь решением
Присоединяйтесь к нам...
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Найдите угол ABC. Ответ дайте в градусах.
В трапеции ABCD известно, что AD=4, BC=3, а её площадь равна 84. Найдите площадь трапеции BCNM, где MN — средняя линия трапеции ABCD.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AOD.
Площадь прямоугольного треугольника равна
722√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: