
Какое из следующих утверждений верно?
1) Все углы ромба равны.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
Рассмотрим каждое утверждение:
1) "Все углы ромба равны". Ромб, у которого все углы равны - это уже
квадрат. Не каждый
ромб является
квадратом, следовательно данное утверждение неверно.
2) "Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны" - это утверждение неверно. Можно привести простой пример:
квадрат и
ромб с равными сторонами - стороны равны, а четырехугольники не равны.
3) "Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности" - это утверждение верно по
второму свойству касательной.
Ответ: 3)
Поделитесь решением
Присоединяйтесь к нам...
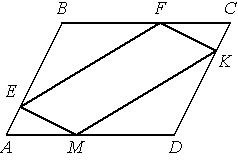 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
 Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=9. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=9. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
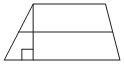 Основания трапеции равны 2 и 6, а высота равна 3. Найдите среднюю линию этой трапеции.
Основания трапеции равны 2 и 6, а высота равна 3. Найдите среднюю линию этой трапеции.
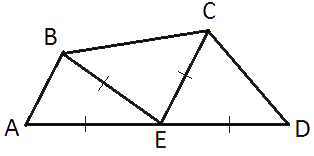 Середина E стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 92° и 148°.
Середина E стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 92° и 148°.
Комментарии: