Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=25°. Найдите величину угла BOC. Ответ дайте в градусах.
Так как треугольник ABC
равнобедренный, то:
∠BAC=∠BCA=x (по
свойству равнобедренного треугольника)
По
теореме о сумме углов треугольника:
180°=∠BAC+∠BCA+∠ABC
180°=x+x+25°
155°=2x
x=77,5°=∠BAC
∠BAC -
вписанный в окружность угол, следовательно градусная мера дуги, на которую он опирается (дуга BC) вдвое больше самого угла:
2*77,5°=155°
∠BOC -
центральный угол, следовательно, он равен градусной мере дуги, на которую он опирается, т.е. 155°
Ответ: 155
Поделитесь решением
Присоединяйтесь к нам...
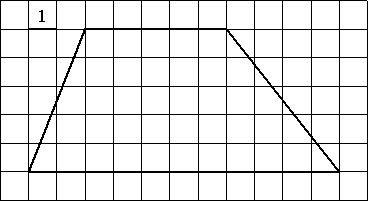Найдите площадь трапеции, изображённой на рисунке.
На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=12, BC=18 и CD=8.
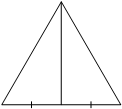Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
Хорды AC и BD окружности пересекаются в точке P, BP=7, CP=14, DP=10. Найдите AP.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=28, AC=24, MN=18. Найдите AM.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: