В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=3 и CH=1. Найдите cosB.
Треугольник ABH
прямоугольный (т.к. AH -
высота).
Тогда cosB=BH/AB (по
определению).
AB=BC (по условию).
BC=BH+CH=3+1=4=AB
cosB=BH/AB=3/4=0,75
Ответ: 0,75
Поделитесь решением
Присоединяйтесь к нам...
Человек, рост которого равен 2 м, стоит на расстоянии 3,5 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
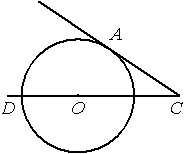Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
130°.
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
2) Диагонали ромба точкой пересечения делятся пополам.
3) Из двух хорд окружности больше та, середина которой находится дальше от центра окружности.
Окружности радиусов 3 и 33 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 5 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: