Автор: Таська
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 57.
Для удобства введем обозначения:
a - сторона
ромба (они равны по
определению ромба)
d - диагональ AC
57d - диагональ BD (по условию)
AE - k
EB - t
Площадь
параллелограмма через диагонали равна BD*AC*sinα/2 = 57d*d*sinα/2 = 28,5d2*sinα, где α - угол между диагоналями (при чем не важно какой, так как синусы обоих углов будут равны друг другу).
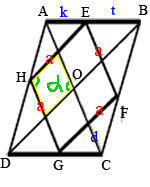Так как стороны
ромба параллельны диагоналям, образуется маленький
параллелограмм, а значит противоположные углы равны (по
свойству параллелограмма).
Рассмотрим треугольники ABC и EBF.
∠EBF - общий
∠BFE=∠BCA (это
соответственные углы)
Следовательно, треугольники ABC и EBF
подобны (по
первому признаку подобия).
Тогда EF/AC=a/d=t/(t+k)
Аналогично,
подобны и треугольники ABD и AEH.
Для них справедливо: a/57d=k/(t+k)
Складываем эти два уравнения:
a/d+a/57d=t/(t+k)+k/(t+k)
57a/57d+a/57d=(t+k)/(t+k)
58a/57d=1
58a=57d
a=57d/58
Sромба=a2sinα
Sпараллелограмма=28,5d2*sinα (это мы выяснили ранее)
Sромба/Sпараллелограмма=(a2sinα)/(28,5d2*sinα)=a2/(28,5d2)=(57d/58)2/(28,5d2)=(572*d2)/(582*28,5*d2)=3249/(3364*28,5)=114/3364=57/1682
Ответ: 57/1682
Поделитесь решением
Присоединяйтесь к нам...
Катеты прямоугольного треугольника равны 4√
Укажите номера верных утверждений.
1) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
2) Смежные углы равны.
3) Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника ABC.
Площадь прямоугольного треугольника равна 2√
Синус острого угла A треугольника ABC равен 
. Найдите CosA.
Хочу получать новые решения
Ни какого спама
Комментарии: