
 Площадь прямоугольного треугольника равна 2√
Площадь прямоугольного треугольника равна 2√
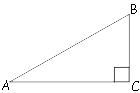 Площадь
прямоугольного треугольника равна половине произведения катетов:
Площадь
прямоугольного треугольника равна половине произведения катетов:
S=AC*BC/2
Пусть 30-и градусам равен угол BAC.
Тангенс BAC:
td∠BAC=tg30°=BC/AC=√
BC=AC√
S=AC*(AC√
AC2/2=2
AC2=4
AC=2
Ответ: 2
Поделитесь решением
Присоединяйтесь к нам...
 Сторона ромба равна 40, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 40, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=17 и MB=19. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=17 и MB=19. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
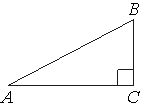 В треугольнике ABC угол C равен 90°, AC=24, AB=25. Найдите sinB.
В треугольнике ABC угол C равен 90°, AC=24, AB=25. Найдите sinB.
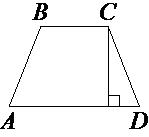 Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.
 Радиус окружности, описанной около квадрата, равен 14√
Радиус окружности, описанной около квадрата, равен 14√
Комментарии: