
 В трапеции ABCD AB=CD, ∠BDA=49° и ∠BDC=13°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, ∠BDA=49° и ∠BDC=13°. Найдите угол ABD. Ответ дайте в градусах.
∠ADC=∠BDA+∠BDC=49°+13°=62°.
Трапеция ABCD -
равнобедренная (т.к. AB=CD), следовательно, по
свойству равнобедренной трапеции, ∠BAD=∠ADC=62°.
Рассмотрим треугольник ABD:
По
теореме о сумме углов треугольника:
180°=∠BAD+∠ABD+∠BDA
180°=62°+∠ABD+49°
∠ABD=180°-62°-49°
∠ABD=69°
Ответ: 69
Поделитесь решением
Присоединяйтесь к нам...
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=66, AC=44, MN=24. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=66, AC=44, MN=24. Найдите AM.
 Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь этого треугольника.
Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь этого треугольника.
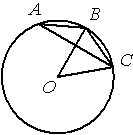 Точка О – центр окружности, /BAC=10° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=10° (см. рисунок). Найдите величину угла BOC (в градусах).
 Площадь прямоугольного треугольника равна 800√
Площадь прямоугольного треугольника равна 800√
 В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.
Комментарии: