
 Биссектрисы углов B и C трапеции ABCD пересекаются в точке O, лежащей на стороне AD. Докажите, что точка O равноудалена от прямых AB, BC и CD.
Биссектрисы углов B и C трапеции ABCD пересекаются в точке O, лежащей на стороне AD. Докажите, что точка O равноудалена от прямых AB, BC и CD.
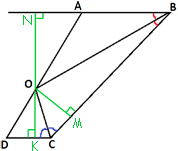 Расстояние от точки О до прямых - это длина перпендикуляра, проведенного от точки до прямой. Иными словами, надо доказать, что ON=OM=OK.
Расстояние от точки О до прямых - это длина перпендикуляра, проведенного от точки до прямой. Иными словами, надо доказать, что ON=OM=OK.
Рассмотрим треугольник NBO.
sin∠NBO=ON/OB (по
определению синуса).
ON=OB*sin∠NBO
Рассмотрим треугольник BMO.
sin∠OBM=OM/OB (по
определению синуса).
OM=OB*sin∠OBM
∠NBO=∠OBM (т.к. OB -
биссектриса).
Следовательно, OM=OB*sin∠OBM=OB*sin∠NBO=ON
Аналогично доказывается, что OK=OM.
Т.е. ON=OM=OK.
Поделитесь решением
Присоединяйтесь к нам...
 Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,8 м, высота большой опоры 2,8 м. Найдите высоту средней опоры.
Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,8 м, высота большой опоры 2,8 м. Найдите высоту средней опоры.
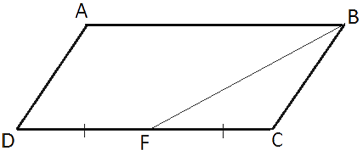 Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка F — середина стороны CD. Докажите, что BF — биссектриса угла ABC.
Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка F — середина стороны CD. Докажите, что BF — биссектриса угла ABC.
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=12, BF=5.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=12, BF=5.
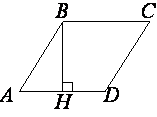 Высота BH ромба ABCD делит его сторону AD на отрезки AH=44 и HD=11. Найдите площадь ромба.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=44 и HD=11. Найдите площадь ромба.
 Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 25, а основание BC равно 5. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 25, а основание BC равно 5. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Комментарии: