
 В треугольнике ABC проведена биссектриса AL, угол ALC равен 152°, угол ABC равен 137°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 152°, угол ABC равен 137°. Найдите угол ACB. Ответ дайте в градусах.
Пусть ∠BAL=x
Тогда, ∠LAC тоже =x (так как AL -
биссектриса).
Рассмотрим треугольник ABC:
∠ABC+∠ACB+∠CAB=180° (по
теореме о сумме углов треугольника).
137°+∠ACB+2x=180°
∠ACB+2x=43°
x=(43°-∠ACB)/2
Рассмотрим треугольник ALC:
∠ALC+∠ACB+∠LAC=180° (по
теореме о сумме углов треугольника).
152°+∠ACB+x=180°
∠ACB+x=28°
Подставляем значение x, полученное ранее:
∠ACB+(43°-∠ACB)/2=28° |*2
2∠ACB+43°-∠ACB=56°
∠ACB=56°-43°=13°
Ответ: 13
Поделитесь решением
Присоединяйтесь к нам...
 Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
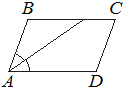 Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
 Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB=26.
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB=26.
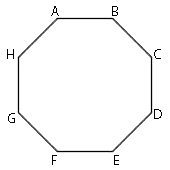 ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
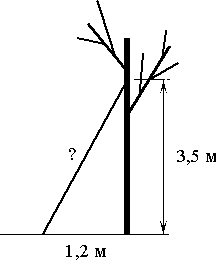 Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 3,5 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?
Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 3,5 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?
Комментарии: