
 Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 62°, 54° и 64°.
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 62°, 54° и 64°.
Пусть:
∠KMP=62°
∠MKP=54°
∠KPM=64°
Рассмотрим треугольник AMK.
AM=AK (по
второму свойству касательной)
Следовательно треугольник AMK -
равнобедренный, тогда, по
свойству равнобедренного треугольника:
∠AMK=∠AKM
Заметим, что оба этих угла охватывают дугу MK, и следовательно равны половине ее градусной меры (по
свойству углов на окружности).
∠KPM является
вписанным в окружность углом и опирается на эту же дугу, следовательно и он равен половине градусной меры этой дуги.
Получается, что:
∠AMK=∠AKM=∠KPM=64°
Применив
теорему о сумме углов треугольника:
180°=∠AMK+∠AKM+∠MAK
180°=64°+64°+∠MAK
∠MAK=52°
Аналогично, для двух других треугольников получим:
∠BKP=∠BPK=∠KMP=62°
∠KBP=180°-62°-62°=56°
И...
∠CPM=∠CMP=∠MKP=54°
∠PCM=180°-54°-54°=72°
Ответ: 52°, 56° и 72°
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 92. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 92. Найдите стороны треугольника ABC.
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
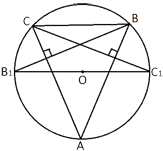 Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
2) Диагонали ромба точкой пересечения делятся пополам.
3) Из двух хорд окружности больше та, середина которой находится дальше от центра окружности.
Комментарии: