
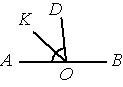
 Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=108°. Ответ дайте в градусах.
Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=108°. Ответ дайте в градусах.
∠AOD=180°-∠DOB=180°-108°=72° (так как ∠AOB - развернутый, т.е. равен 180°).
Так как OK - биссектриса, то ∠DOK=∠AOD/2=72°/2=36°
Ответ: 36
Поделитесь решением
Присоединяйтесь к нам...
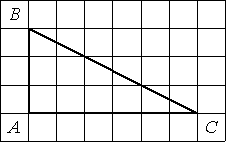 Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
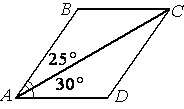 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
 Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=2. Найдите высоту ромба.
Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=2. Найдите высоту ромба.
 Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 20, а площадь равна 50√
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 20, а площадь равна 50√
 Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 3:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 41.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 3:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 41.
Комментарии: