
 Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=25, BC=15, CF:DF=3:2.
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=25, BC=15, CF:DF=3:2.
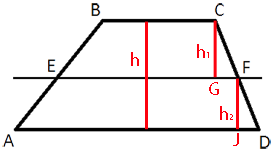 Проведем
высоты h1 и h2 как показано на рисунке.
Проведем
высоты h1 и h2 как показано на рисунке.
Рассмотрим треугольники CFG и FDJ.
∠CGF=∠FJD=90° (т.к. мы проводили
высоты).
∠CFG=∠FDJ (т.к. это
соответственные углы).
Следовательно, эти треугольники
подобны по
первому признаку подобия.
По
определению подобных треугольников:
CF/DF=CG/FJ=3/2
Для простоты обозначим:
CG=h1
FJ=h2
SEBCF=(CB+EF)*h1/2
SAEFD=(EF+AD)*h2/2
SABCD=(BC+AD)*(h1+h2)/2
Так сумма площадей этих
трапеций равна площади большой трапеции, то запишем:
(CB+EF)*h1/2+(EF+AD)*h2/2=(BC+AD)*(h1+h2)/2
(CB+EF)*h1+(EF+AD)*h2=(BC+AD)*(h1+h2)
(CB+EF)*h1+(EF+AD)*h2=(BC+AD)*h1+(BC+AD)*h2
(CB+EF)*h1-(BC+AD)*h1=(BC+AD)*h2-(EF+AD)*h2
(CB+EF-BC-AD)*h1=(BC+AD-EF-AD)*h2
(EF-AD)*h1=(BC-EF)*h2
h1/h2=(BC-EF)/(EF-AD)
3/2=(15-EF)/(EF-25)
3(EF-25)=2(15-EF)
3*EF-75=30-2*EF
5*EF=105
EF=21
Ответ: EF=21
Поделитесь решением
Присоединяйтесь к нам...
Стороны AC, AB, BC треугольника ABC равны 3√
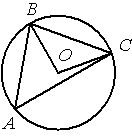 Точка О – центр окружности, /BOC=100° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=100° (см. рисунок). Найдите величину угла BAC (в градусах).
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
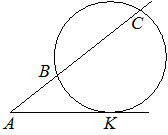 Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=4, AC=64. Найдите AK.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=4, AC=64. Найдите AK.
Укажите номера верных утверждений.
1) Если один из углов треугольника прямой, то треугольник прямоугольный.
2) Диагонали квадрата точкой пересечения делятся пополам.
3) Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
Комментарии: