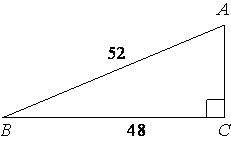ОГЭ, Математика.
Геометрия: Задача №FC0269

Задача №577 из 1087
Условие задачи:

Найдите площадь треугольника, изображённого на рисунке.

Решение задачи:

Площадь прямоугольного треугольника S=AC*BC/2
Найдем AC по теореме Пифагора:
AB²=AC²+BC²
52²=AC²+48²
AC²=2704-2304=400
AC=20
S_ABC=20*48/2=480
Ответ: S_ABC=480

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №060A64

В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA=NA. Докажите, что данный параллелограмм — прямоугольник.

Задача №96E95A

Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.

Задача №246BF7

Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.