
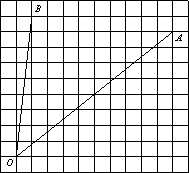
 Найдите тангенс угла
AOB.
Найдите тангенс угла
AOB.
Вариант №1 (Прислал пользователь Евгений)
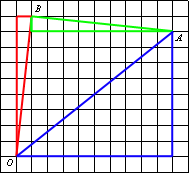 Проведем отрезок AB.
Проведем отрезок AB.
Найдем каждую сторону треугольника ABO по
теореме Пифагора:
AO2=102+82
AO2=100+64=164
AO=√
AB2=92+12
AB2=81+1=82
AB=√
BO2=92+12
BO2=81+1=82
BO=√
По
теореме косинусов:
AB2=AO2+BO2-2AO*BO*cos∠AOB
(√
82=164+82-2√
-164=-2√
82=√
82=2√
41=√
cos∠AOB=41/√
По основной тригонометрической формуле:
sin2∠AOB+cos2∠AOB=1
sin2∠AOB+(1/√
sin2∠AOB+1/2=1
sin2∠AOB=1/2
sin∠AOB=1/√
tg∠AOB=sin∠AOB/cos∠AOB=(1/√
Ответ: tg∠AOB=1
 Достроим чертеж до двух
прямоугольных треугольников. Найдем
тангенсы для обоих треугольников для их углов О.
Достроим чертеж до двух
прямоугольных треугольников. Найдем
тангенсы для обоих треугольников для их углов О.Поделитесь решением
Присоединяйтесь к нам...
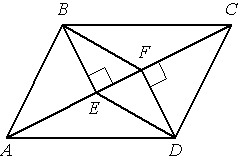 В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ — параллелограмм.
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ — параллелограмм.
 На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E . Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E . Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.
 В треугольнике ABC AC=15, BC=5√
В треугольнике ABC AC=15, BC=5√
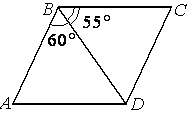 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
60° и 55°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
60° и 55°. Найдите меньший угол параллелограмма.
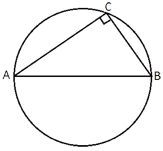
 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.
Комментарии: