Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD=36.
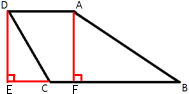Дочертим отрезки как показано на рисунке.
DE=AF, т.к. это
высоты
трапеции.
∠DCE=180°-∠BCD=180°-135°=45° (т.к. это
смежные углы).
sin(∠DCE)=ED/CD (по
определению)
sin45°=ED/CD (sin45°=√
√
ED=36√
sin(∠ABF)=AF/AB (по
определению)
sin60°=ED/AB
AB=ED/sin60° (sin60°=√
AB=(18√
Ответ: AB=12√
Поделитесь решением
Присоединяйтесь к нам...
Найдите площадь параллелограмма, изображённого на рисунке.
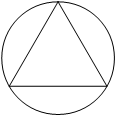Радиус окружности, описанной около равностороннего треугольника, равен 2√
Боковые стороны AB и CD трапеции ABCD равны соответственно 18 и 30, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Укажите номера верных утверждений.
1) Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Ромб не является параллелограммом.
3) Сумма острых углов прямоугольного треугольника равна 90°.
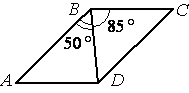Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
50° и 85°. Найдите меньший угол параллелограмма.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: