Точка O – центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR – ромб. Найдите угол ORQ. Ответ дайте в градусах.
FO=RO (т.к. это радиусы окружности)
FO=RO=FQ=QR (по
определению ромба)
Проведем отрезок OQ.
OQ тоже радиус окружности, следовательно OQ=FO=RO=FQ=QR
Следовательно, треугольники FQO и QRO -
равносторонние, а все углы равностороннего треугольника равны 60° (по
свойству).
Следовательно, /ORQ=60°
Ответ: 60
Поделитесь решением
Присоединяйтесь к нам...
В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 30°. Найдите величину угла OAB.
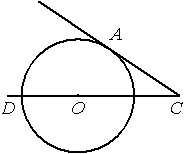Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
130°.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=12 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
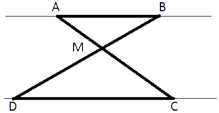Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=16, DC=24, AC=25.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 4. Найдите площадь трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: