
 Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=13.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=13.
Решение прислал один из наших пользователей, имя не известно.
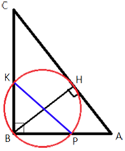 ∠KBP=90° (по условию)
∠KBP=90° (по условию)
Прямоугольный треугольник KPB с гипотенузой PK вписан в окружность.
Следовательно, PK является диаметром окружности. (по
теореме об описанной окружности).
KP=BH=13
Ответ: PK=13
Поделитесь решением
Присоединяйтесь к нам...
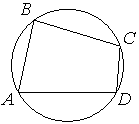 Угол A четырёхугольника ABCD, вписанного в окружность, равен 82°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Угол A четырёхугольника ABCD, вписанного в окружность, равен 82°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
 Площадь прямоугольного треугольника равна 2√
Площадь прямоугольного треугольника равна 2√
 Радиус окружности, вписанной в трапецию, равен 32. Найдите высоту этой трапеции.
Радиус окружности, вписанной в трапецию, равен 32. Найдите высоту этой трапеции.
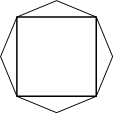 Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
Какие из данных утверждений верны? Запишите их номера.
1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
2) Треугольник со сторонами 1, 2, 4 не существует.
3) Сумма квадратов диагоналей прямоугольника равна сумме квадратов всех его сторон.
Комментарии: