
 Высота равностороннего треугольника равна 96√
Высота равностороннего треугольника равна 96√
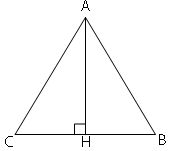 AB=BC=AC (т.к. треугольник
равносторонний)
AB=BC=AC (т.к. треугольник
равносторонний)
Периметр равен: P=AB+BC+CA=3AC
AH -
высота, по
свойству равностороннего треугольника, она так же является и
медианой, и
биссектрисой.
Следовательно, BH=CH=BC/2=AC/2
По
теореме Пифагора:
AC2=AH2+CH2
AC2=AH2+(AC/2)2
AC2-AC2/4=(96√
3*AC2/4=962*3
AC2/4=962
AC2=(2*96)2
AC=2*96=192
P=3AC=3*192=576
Ответ: P=576
Поделитесь решением
Присоединяйтесь к нам...
 Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
 Площадь прямоугольного треугольника равна 8√
Площадь прямоугольного треугольника равна 8√
 Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.
 На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
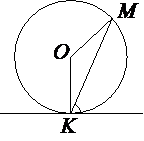 Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 84°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 84°. Найдите величину угла OMK. Ответ дайте в градусах.
Комментарии: