
 Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
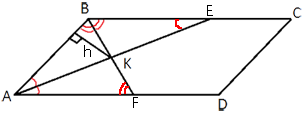 Обозначим точки пересечения
биссектрис со сторонами как показано на рисунке.
Обозначим точки пересечения
биссектрис со сторонами как показано на рисунке.
∠FAK=∠BEK (т.к. это
накрест-лежащие углы).
Получается, что ∠BAK=∠BEK, следовательно треугольник ABE -
равнобедренный (по
свойству равнобедренного треугольника).
Тогда AB=BE.
Треугольники ABK и EBK равны по
первому признаку равенства треугольников.
Следовательно и
высоты у этих треугольников тоже равны.
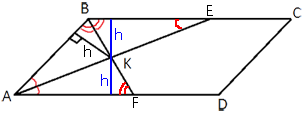 Аналогично, равны и треугольники ABK и AFK.
Аналогично, равны и треугольники ABK и AFK.
Получается, что высота
параллелограмма равна 2h.
Площадь
параллелограмма равна SABCD=2h*BC=2*3*11=66
Ответ: SABCD=66
Поделитесь решением
Присоединяйтесь к нам...
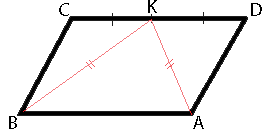 В параллелограмме ABCD точка K — середина стороны CD. Известно, что KA=KB. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD точка K — середина стороны CD. Известно, что KA=KB. Докажите, что данный параллелограмм — прямоугольник.
 Радиус окружности, вписанной в равнобедренную трапецию, равен 20. Найдите высоту этой трапеции.
Радиус окружности, вписанной в равнобедренную трапецию, равен 20. Найдите высоту этой трапеции.
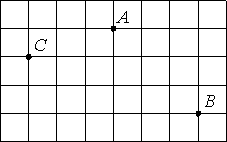 На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.
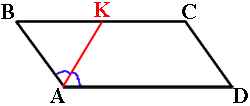 Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=6, CK=10.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=6, CK=10.
Комментарии: