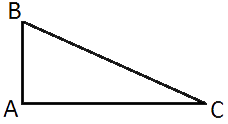
В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
SABC=AB*AC/2
Пусть угол, равный 45° будет угол В.
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
180°=90°+45°+∠C
∠C=45°
Следовательно, по
свойству равнобедренного треугольника, треугольник ABC -
равнобедренный.
Значит AB=AC.
По
теореме Пифагора:
BC2=AB2+AC2
BC2=AB2+AB2
702=2AB2
4900=2AB2
AB2=2450
SABC=AB*AC/2
SABC=AB2/2=2450/2=1225
Ответ: SABC=1225
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 18. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
В треугольнике ABC AB=BC=53, AC=56. Найдите длину медианы BM.
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 8. Найдите площадь четырёхугольника ABMN.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2024-02-11 01:22:37) Кристина: Найдите площадь прямоугольного треугольника, если его катет и гипоте- нуза равны соответственно 12 и 13.