В треугольнике ABC DE – средняя линия. Площадь треугольника CDE равна 35. Найдите площадь треугольника ABC.
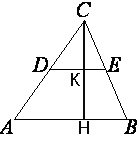Проведем
высоту CH.
Средняя линия делит CH пополам, как и стороны треугольника.
Следовательно, CK=KH.
По
теореме о средней линии AB=2DE.
SCDE=DE*CK/2=35.
DE*CK=70
SABC=AB*CH/2=2DE*2CK/2=2DE*CK=2*70=140
Ответ: SABC=140
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах.
Косинус острого угла A треугольника ABC равен 
. Найдите sinA.
Человек ростом 1,5 м стоит на расстоянии 7 м от столба, на котором висит фонарь на высоте 3,6 м. Найдите длину тени человека в метрах.
В треугольнике ABC AC=15, BC=5√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: