
 В треугольнике ABC угол C равен 90°, sinA=7/17, AC=4√
В треугольнике ABC угол C равен 90°, sinA=7/17, AC=4√
По
определению: sinA=BC/AB => BC=AB*sinA=AB*7/17
По
теореме Пифагора:
AB2=BC2+AC2
AB2=(AB*7/17)2+(4√
AB2-(AB*7/17)2=16*15
AB2(1-(7/17)2)=240
AB2(289/289-49/289)=240
AB2*240/289=240
AB2=289
AB=17
Ответ: AB=17
Поделитесь решением
Присоединяйтесь к нам...
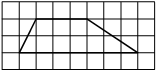 На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите её площадь.
На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите её площадь.
 Прямая, параллельная стороне
AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.
Прямая, параллельная стороне
AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.
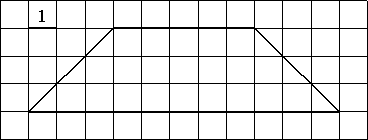 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
 В трапеции ABCD AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.
 Радиус вписанной в квадрат окружности равен 24√2. Найдите радиус окружности, описанной около этого квадрата.
Радиус вписанной в квадрат окружности равен 24√2. Найдите радиус окружности, описанной около этого квадрата.
Комментарии:
(2015-05-24 20:34:29) Администратор: Катя, мы AB2 вынесли за скобки.
(2015-05-24 20:20:41) Катя: почему на шестой строке в решении написано 1 вместо АВ? Поясните решение на шестой строчке)