
 Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=7, CK=12.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=7, CK=12.
Периметр
параллелограмма:
P=AB+BC+CD+AD
AB=CD и BC=AD (по
свойству параллелограмма)
P=AB+BC+AB+BC=2(AB+BC)
∠DAK=∠AKB (т.к. это
накрест-лежащие углы).
Следовательно ∠AKB=∠KAB (т.к. AK -
биссектриса)
Получается, что треугольник ABK -
равнобедренный (по
свойству равнобедренного треугольника).
Тогда AB=BK=7
P=2(AB+BC)=2(AB+BK+KC)=2(7+7+12)=52
Ответ: P=52
Поделитесь решением
Присоединяйтесь к нам...
 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 25°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 25°. Найдите больший угол параллелограмма.
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=28, AC=24, MN=18. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=28, AC=24, MN=18. Найдите AM.
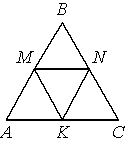 В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что АMNK — ромб.
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что АMNK — ромб.
Две трубы, диаметры которых равны 7 см и 24 см, требуется заменить одной, площадь поперечного сечения которой равна сумме площадей поперечных сечений двух данных. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.
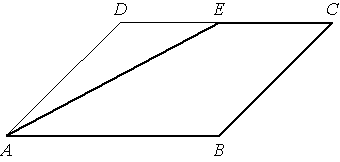 Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Комментарии: