
 Площадь прямоугольного треугольника равна 32√
Площадь прямоугольного треугольника равна 32√
Площадь
прямоугольного треугольника равна половине произведения катетов:
S=AC*BC/2=32√
Пусть 60-и градусам равен угол BAC.
Котангенс BAC:
ctd∠BAC=ctg60°=AC/BC=√
AC=BC√
S=AC*BC/2=32√
AC*BC=64√
BC*BC√
BC2=64
BC=8
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
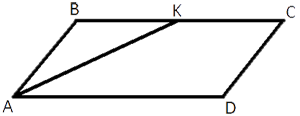 Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
 Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
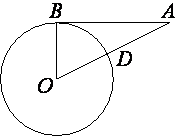 Отрезок AB=32 касается окружности радиуса 24 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Отрезок AB=32 касается окружности радиуса 24 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
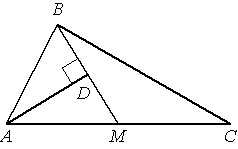 Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
 В треугольнике со сторонами 15 и 3 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
В треугольнике со сторонами 15 и 3 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
Комментарии: