
 Площадь прямоугольного треугольника равна 968√
Площадь прямоугольного треугольника равна 968√
Площадь
прямоугольного треугольника равна половине произведения катетов:
S=AC*BC/2=968√
Пусть 60-и градусам равен угол BAC.
Тангенс BAC:
td∠BAC=tg60°=BC/AC=√
BC=AC√
S=AC*BC/2=968√
AC*BC=1936√
AC*AC√
AC2=1936
AC=44
Ответ: 44
Поделитесь решением
Присоединяйтесь к нам...
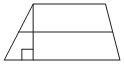 Основания трапеции равны 2 и 6, а высота равна 3. Найдите среднюю линию этой трапеции.
Основания трапеции равны 2 и 6, а высота равна 3. Найдите среднюю линию этой трапеции.
 Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC=34.
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC=34.
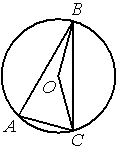 Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
 Сторона AB параллелограмма ABCD вдвое больше стороны AD. Точка K — середина стороны AB. Докажите, что DK — биссектриса угла ADC.
Сторона AB параллелограмма ABCD вдвое больше стороны AD. Точка K — середина стороны AB. Докажите, что DK — биссектриса угла ADC.
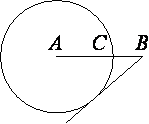 На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
Комментарии:
(2017-02-14 20:10:36) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2017-02-14 17:05:40) : в прямоугольном треугольнике гепотинуза ровна 3 см один из острых углов равен 60 градусов найти катеты треугольника