
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ43 –ł–∑ 1087 |
 –í –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ O –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ—č –ī–ł–į–ľ–Ķ—ā—Ä—č
AD –ł BC, —É–≥–ĺ–Ľ OAB —Ä–į–≤–Ķ–Ĺ 70¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—É —É–≥–Ľ–į OCD.
–í –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ O –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ—č –ī–ł–į–ľ–Ķ—ā—Ä—č
AD –ł BC, —É–≥–ĺ–Ľ OAB —Ä–į–≤–Ķ–Ĺ 70¬į. –Ě–į–Ļ–ī–ł—ā–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—É —É–≥–Ľ–į OCD.
–í–į—Ä–ł–į–Ĺ—ā ‚ĄĖ1 –ü—Ä–Ķ–ī–Ľ–ĺ–∂–ł–Ľ –Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā–Ķ–Ľ—Ć –ď–ĺ—ą–į.
–ě—á–Ķ–≤–ł–ī–Ĺ–ĺ, —á—ā–ĺ —É–≥–ĺ–Ľ OAB —ć—ā–ĺ —É–≥–ĺ–Ľ DAB, –į ∠DAB —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≤–Ņ–ł—Ā–į–Ĺ–Ĺ—č–ľ –ł –ĺ–Ņ–ł—Ä–į–Ķ—ā—Ā—Ź –Ĺ–į –ī—É–≥—É BD.
∠OCD —ā–ĺ–∂–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≤–Ņ–ł—Ā–į–Ĺ–Ĺ—č–ľ –ł –ĺ–Ņ–ł—Ä–į–Ķ—ā—Ā—Ź –Ĺ–į –ī—É–≥—É BD.
–Ę–ĺ–≥–ī–į, –Ņ–ĺ —ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –ĺ –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–ľ —É–≥–Ľ–Ķ, —ć—ā–ł —É–≥–Ľ—č —Ä–į–≤–Ĺ—č:
∠OCD=∠OAB=70¬į.
–ě—ā–≤–Ķ—ā: 70
–í–į—Ä–ł–į–Ĺ—ā ‚ĄĖ2
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ –ź–ě–í. –≠—ā–ĺ—ā —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ
—Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ—č–Ļ, —ā.–ļ. –ě–ź –ł –ě–í - —Ä–į–ī–ł—É—Ā—č, –Ņ–ĺ—ć—ā–ĺ–ľ—É –ĺ–Ĺ–ł —Ä–į–≤–Ĺ—č.
–ü–ĺ
—Ā–≤–ĺ–Ļ—Ā—ā–≤—É —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ∠OAB=∠OBA.
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł –ź–ě–í –ł COD. ∠DOC=∠AOB, —ā.–ļ. –ĺ–Ĺ–ł
–≤–Ķ—Ä—ā–ł–ļ–į–Ľ—Ć–Ĺ—č–Ķ. –°–ě=DO=OB=OA, —ā.–ļ. —ć—ā–ĺ —Ä–į–ī–ł—É—Ā—č –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł.
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł –ź–ě–í –ł COD —Ä–į–≤–Ĺ—č (–Ņ–ĺ –Ņ–Ķ—Ä–≤–ĺ–ľ—É –Ņ—Ä–ł–∑–Ĺ–į–ļ—É). –ü–ĺ—ć—ā–ĺ–ľ—É ∠OBA=∠OAB=∠ODC=∠OCD=70¬į
–ě—ā–≤–Ķ—ā: 70
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
 –í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ ∠BAC=64¬į, AD ‚ÄĒ –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ BAD. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ ∠BAC=64¬į, AD ‚ÄĒ –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ BAD. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–Ě–į –ļ–į–ļ–ĺ–Ļ —É–≥–ĺ–Ľ (–≤ –≥—Ä–į–ī—É—Ā–į—Ö) –Ņ–ĺ–≤–ĺ—Ä–į—á–ł–≤–į–Ķ—ā—Ā—Ź –ľ–ł–Ĺ—É—ā–Ĺ–į—Ź —Ā—ā—Ä–Ķ–Ľ–ļ–į, –Ņ–ĺ–ļ–į —á–į—Ā–ĺ–≤–į—Ź –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā 11¬į?
 –í —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ AD –≤–ī–≤–ĺ–Ķ –Ī–ĺ–Ľ—Ć—ą–Ķ –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź –í–° –ł –≤–ī–≤–ĺ–Ķ –Ī–ĺ–Ľ—Ć—ą–Ķ –Ī–ĺ–ļ–ĺ–≤–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č CD. –£–≥–ĺ–Ľ ADC —Ä–į–≤–Ķ–Ĺ 60¬į, —Ā—ā–ĺ—Ä–ĺ–Ĺ–į AB —Ä–į–≤–Ĺ–į 6. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–į–Ņ–Ķ—Ü–ł–ł.
–í —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ AD –≤–ī–≤–ĺ–Ķ –Ī–ĺ–Ľ—Ć—ą–Ķ –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź –í–° –ł –≤–ī–≤–ĺ–Ķ –Ī–ĺ–Ľ—Ć—ą–Ķ –Ī–ĺ–ļ–ĺ–≤–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č CD. –£–≥–ĺ–Ľ ADC —Ä–į–≤–Ķ–Ĺ 60¬į, —Ā—ā–ĺ—Ä–ĺ–Ĺ–į AB —Ä–į–≤–Ĺ–į 6. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–į–Ņ–Ķ—Ü–ł–ł.
–£–ļ–į–∂–ł—ā–Ķ –Ĺ–ĺ–ľ–Ķ—Ä–į –≤–Ķ—Ä–Ĺ—č—Ö —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ļ.
1) –ē—Ā–Ľ–ł —ā—Ä–ł —Ā—ā–ĺ—Ä–ĺ–Ĺ—č –ĺ–ī–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł–ĺ–Ĺ–į–Ľ—Ć–Ĺ—č —ā—Ä—Ď–ľ —Ā—ā–ĺ—Ä–ĺ–Ĺ–į–ľ –ī—Ä—É–≥–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į, —ā–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł –Ņ–ĺ–ī–ĺ–Ī–Ĺ—č.
2) –°—É–ľ–ľ–į —Ā–ľ–Ķ–∂–Ĺ—č—Ö —É–≥–Ľ–ĺ–≤ —Ä–į–≤–Ĺ–į 180¬į.
3) –õ—é–Ī–į—Ź –≤—č—Ā–ĺ—ā–į —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ķ–≥–ĺ –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–ĺ–Ļ.
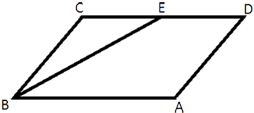 –ü–Ľ–ĺ—Č–į–ī—Ć –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į
ABCD —Ä–į–≤–Ĺ–į 30. –Ę–ĺ—á–ļ–į E ‚Äď —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ—č CD. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABED.
–ü–Ľ–ĺ—Č–į–ī—Ć –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į
ABCD —Ä–į–≤–Ĺ–į 30. –Ę–ĺ—á–ļ–į E ‚Äď —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ—č CD. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABED.
–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł:
(2019-06-03 21:42:10) –ź–ī–ľ–ł–Ĺ–ł—Ā—ā—Ä–į—ā–ĺ—Ä: –ď–ĺ—ą–į, –ī–į, –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ. –≠–Ľ–Ķ–≥–į–Ĺ—ā–Ĺ–ĺ –ł –Ņ—Ä–ĺ—Ā—ā–ĺ. –ě–Ī—Ź–∑–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ —Ā–ļ–ĺ—Ä–ĺ —Ä–į–∑–ľ–Ķ—Č—É —ā–į–ļ–ĺ–Ķ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –Ņ–ĺ–ī –í–į—ą–ł–ľ –ł–ľ–Ķ–Ĺ–Ķ–ľ. –°–Ņ–į—Ā–ł–Ī–ĺ!
(2019-06-03 12:10:28) –≥–ĺ—ą–į: –ź —Ä–į–∑–≤–Ķ –Ĺ–Ķ–Ľ—Ć–∑—Ź —Ā—Ä–į–∑—É –∑–į–ļ–Ľ—é—á–ł—ā—Ć, —á—ā–ĺ —ć—ā–ĺ—ā —É–≥–ĺ–Ľ —Ä–į–≤–Ķ–Ĺ 70 –≥—Ä–į–ī—É—Ā–į–ľ, —ā–į–ļ –ļ–į–ļ –ĺ–Ņ–ł—Ä–į–Ķ—ā—Ā—Ź –Ĺ–į —ā—É –∂–Ķ –ī—É–≥—É —á—ā–ĺ –ł –ī–į–Ĺ–Ĺ—č–Ļ —É–≥–ĺ–Ľ