
 Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 26:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 7.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 26:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 7.
Пусть AD -
биссектриса, описанная в условии.
BC - сторона, равная 7.
Рассмотрим треугольник ADC.
Для этого треугольника CO -
биссектриса,
По
свойству биссектрисы:
AO/OD=AC/CD=26/1
AC=26*CD
Рассмотрим треугольник ABD.
Для этого треугольника BO -
биссектриса,
По
свойству биссектрисы:
AO/OD=AB/BD=26/1
AB=26*BD
Складываем полученные равенства:
AC+AB=26*CD+26*BD
AC+AB=26(CD+BD), CD+BD=BC=7
AC+AB=26*7
AC+AB=182
PABC=AC+AB+BC=182+7=189
Ответ: PABC=189
Поделитесь решением
Присоединяйтесь к нам...
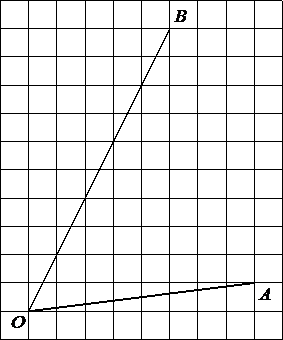 Найдите тангенс угла
AOB.
Найдите тангенс угла
AOB.
 Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
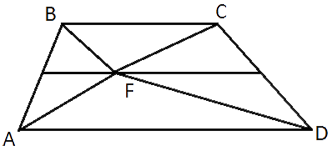 На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
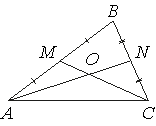 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=33, CM=15. Найдите ON.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=33, CM=15. Найдите ON.
Комментарии: