
 Окружности радиусов 3 и 33 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Окружности радиусов 3 и 33 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
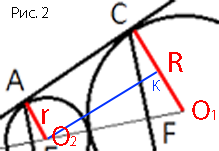
Рассмотрим
трапецию ACO1O2
Данная трапеция
прямоугольная, т.к. радиусы перпендикулярны
касательной AC (по
свойству касательной).
Проведем O2K параллельно AC, O2K=AC, т.к. ACKO2 -
прямоугольник.
 По
теореме Пифагора:
По
теореме Пифагора:
(O1O2)2=(O2K)2+(KO1)2
(R+r)2=(O2K)2+(R-r)2
(33+3)2=(O2K)2+(33-3)2
1296=(O2K)2+900
(O2K)2=396
O2K=6√
Рассмотрим треугольники OAO2 и OCO1 (cм. Рис.1).
∠AOO2 - общий
∠OAO2=∠OCO1=90°
Следовательно эти треугольники
подобны (по
первому признаку подобия треугольников).
Тогда, R/r=OC/OA
33/3=OC/OA=(OA+AC)/OA
11OA=OA+6√
OA=6√
Из
подобия этих же треугольников:
R/r=O10/O2O
R/r=(O2O+R+r)/O2O
33/3=(O2O+33+3)/O2O
11(O2O)=O2O+36
10(O2O)=36
O2O=3,6
Обозначим угол ∠AOO2 как α
cosα=OA/OO2=6√
Посмотрим на треугольники OAE и OCF.
Они
прямоугольные по
второму свойству хорды.
Тогда для треугольника OAE:
cosα=OE/OA
OE=OA*cosα=6√
Для треугольника OCF:
cosα=OF/OC
OF=OC*cosα=(OA+AC)*cosα=(6√
EF=OF-OE=12,1-1,1=11
Ответ: EF=11
Поделитесь решением
Присоединяйтесь к нам...
 Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 230 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 320 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 230 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 320 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
 В окружности с центром в точке O проведены диаметры
AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
В окружности с центром в точке O проведены диаметры
AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника COD.
 Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=13.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=13.
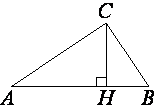 В прямоугольном треугольнике ABC катет AC=65, а высота CH, опущенная на гипотенузу, равна 13√
В прямоугольном треугольнике ABC катет AC=65, а высота CH, опущенная на гипотенузу, равна 13√
Комментарии:
(2017-11-01 22:08:16) Администратор: Марианна, спасибо большое! Опечатка исправлена.
(2017-10-31 09:12:30) Марианна: Опечатка в решении: подобными являются треугольники OAO2 и OCO1 (а не OCO2)