
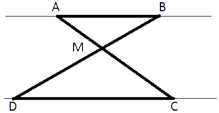 Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=16, DC=24, AC=25.
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=16, DC=24, AC=25.
Рассмотрим треугольники ABM и CDM.
∠AMB=∠CMD (т.к. они
вертикальные).
∠ABM=∠CDM (т.к. они
накрест-лежащие).
Следовательно, треугольники ABM и CDM
подобны (по
первому признаку подобия).
AC=AM+MC => AM=AC-MC
Тогда:
AB/CD=AM/MC
16/24=(AC-MC)/MC
16MC=24(25-MC)
2MC=3(25-MC)
2MC=75-3MC
5MC=75
MC=15
Ответ: MC=15
Поделитесь решением
Присоединяйтесь к нам...
Какие из следующих утверждений верны?
1) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
2) Площадь трапеции равна произведению основания трапеции на высоту.
3) Треугольника со сторонами 1, 2, 4 не существует.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
 В треугольнике ABC AC=BC. Внешний угол при вершине B равен 146°. Найдите угол C . Ответ дайте в градусах.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 146°. Найдите угол C . Ответ дайте в градусах.
 Катеты прямоугольного треугольника равны 8 и 6. Найдите синус наименьшего угла этого треугольника.
Катеты прямоугольного треугольника равны 8 и 6. Найдите синус наименьшего угла этого треугольника.
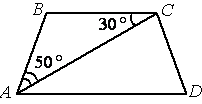 Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные
30° и 50° соответственно.
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные
30° и 50° соответственно.
 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Комментарии: