
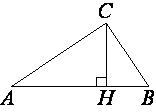
 В прямоугольном треугольнике ABC катет AC=35, а высота CH, опущенная на гипотенузу, равна 14√
В прямоугольном треугольнике ABC катет AC=35, а высота CH, опущенная на гипотенузу, равна 14√
Рассмотрим треугольники ABC и ACH.
∠AHC=∠ACB (т.к. это прямые углы).
∠A - общий.
Следовательно, по
теореме о сумме углов треугольника ∠ACH=∠ABC
Тогда sin∠ACH=sin∠ABC.
Теперь рассмотрим треугольник ACH.
По
теореме Пифагора:
AC2=CH2+AH2
352=(14√
1225=196*6+AH2
AH2=1225-1176
AH2=49
AH=7
sin∠ACH=AH/AC (по
определению)
sin∠ACH=7/35=1/5=0,2
Как было выведено выше:
sin∠ABC=sin∠ACH=0,2
Ответ: sin∠ABC=0,2
Поделитесь решением
Присоединяйтесь к нам...
 Точка H является основанием высоты
BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
Точка H является основанием высоты
BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
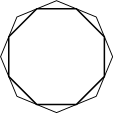 Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
 Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
 Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 11 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=√
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 11 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=√
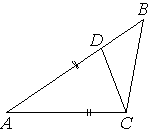 Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=54° и ∠ACB=104°. Найдите угол DCB. Ответ дайте в градусах.
Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=54° и ∠ACB=104°. Найдите угол DCB. Ответ дайте в градусах.
Комментарии: