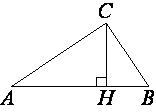
В прямоугольном треугольнике ABC катет AC=35, а высота CH, опущенная на гипотенузу, равна 14√
Рассмотрим треугольники ABC и ACH.
∠AHC=∠ACB (т.к. это прямые углы).
∠A - общий.
Следовательно, по
теореме о сумме углов треугольника ∠ACH=∠ABC
Тогда sin∠ACH=sin∠ABC.
Теперь рассмотрим треугольник ACH.
По
теореме Пифагора:
AC2=CH2+AH2
352=(14√
1225=196*6+AH2
AH2=1225-1176
AH2=49
AH=7
sin∠ACH=AH/AC (по
определению)
sin∠ACH=7/35=1/5=0,2
Как было выведено выше:
sin∠ABC=sin∠ACH=0,2
Ответ: sin∠ABC=0,2
Поделитесь решением
Присоединяйтесь к нам...
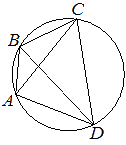Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD основания AD и BC равны соответственно 34 и 9, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=10.
Какие из следующих утверждений верны?
1) Один из двух смежных углов острый, а другой тупой.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.
Прямые m и n параллельны. Найдите ∠3, если ∠1=22°, ∠2=72°. Ответ дайте в градусах.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: