
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=1:4, KM=13.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=1:4, KM=13.
Рассмотрим треугольники ABC и KBM.
/B - общий.
/BAC=/BKM (т.к. это
соответственные углы)
/BCA=/BMK (т.к. это тоже
соответственные углы)
Следовательно, эти треугольники
подобны по
первому признаку подобия.
Тогда по
определению подобных треугольников:
BA/BK=AC/KM
(BK+KA)/BK=AC/KM
1+KA/BK=AC/KM
1+4/1=AC/KM
5=AC/13
AC=5*13=65
Ответ: AC=65
Поделитесь решением
Присоединяйтесь к нам...
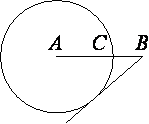 На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
 ABCDEFGHI – правильный девятиугольник. Найдите угол ADC. Ответ дайте в градусах.
ABCDEFGHI – правильный девятиугольник. Найдите угол ADC. Ответ дайте в градусах.
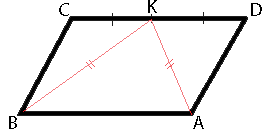 В параллелограмме ABCD точка K — середина стороны CD. Известно, что KA=KB. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD точка K — середина стороны CD. Известно, что KA=KB. Докажите, что данный параллелограмм — прямоугольник.
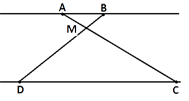 Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=15, DC=30, AC=39.
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=15, DC=30, AC=39.
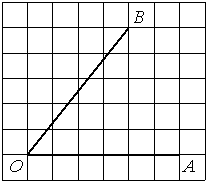 Найдите тангенс угла AOB, изображённого
на рисунке.
Найдите тангенс угла AOB, изображённого
на рисунке.
Комментарии: