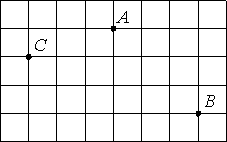
На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
Площадь клетки равна 1, значит клетка имеет и единичные стороны, т.е. равные 1 (1*1=1).
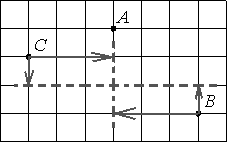Серединой отрезка BC будет будет точка, которая лежит посередине относительно вертикальной и горизонтальной осей.
То есть, относительно точки С на 3 клетки вправо и на одну клетку вниз.
Относительно точки В на 3 клетки влево и на одну клетку вверх.
Тогда очевидно, что расстояние от точки А до середины ВС равно 2
Ответ: расстояние от точки A до середины отрезка BC равно 2
Поделитесь решением
Присоединяйтесь к нам...
Стороны AC, AB, BC треугольника ABC равны 2√
Касательные к окружности с центром O в точках A и B пересекаются под углом 82°. Найдите угол ABO. Ответ дайте в градусах.
Какое из следующих утверждений верно?
1) Все углы ромба равны.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: