
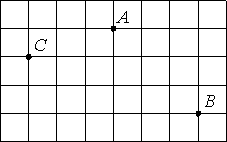
 На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
Площадь клетки равна 1, значит клетка имеет и единичные стороны, т.е. равные 1 (1*1=1).
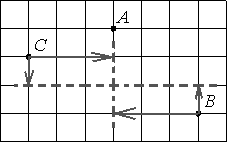 Серединой отрезка BC будет будет точка, которая лежит посередине относительно вертикальной и горизонтальной осей.
Серединой отрезка BC будет будет точка, которая лежит посередине относительно вертикальной и горизонтальной осей.
То есть, относительно точки С на 3 клетки вправо и на одну клетку вниз.
Относительно точки В на 3 клетки влево и на одну клетку вверх.
Тогда очевидно, что расстояние от точки А до середины ВС равно 2
Ответ: расстояние от точки A до середины отрезка BC равно 2
Поделитесь решением
Присоединяйтесь к нам...
 Проектор полностью освещает экран A высотой 190 см, расположенный
на расстоянии 210 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 380 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
Проектор полностью освещает экран A высотой 190 см, расположенный
на расстоянии 210 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 380 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
 Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 62°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 62°. Найдите величину угла OMK. Ответ дайте в градусах.
 В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции.
 В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
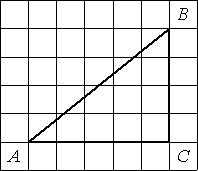 Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Комментарии: