В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 8. Найдите площадь четырёхугольника ABMN.
MN -
средняя линия треугольника ABC, по теореме о средней линии NM=AB/2 => 2NM=AB.
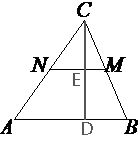Проведем
высоту из вершины С.
SCNM=1/2*CE*NM=8 (по условию).
CE*NM=16
Рассмотрим треугольник ACD, NE||AD и идет из середины стороны AC, следовательно NE -
средняя линия для треугольника ACD, значит CE=ED.
ABMN - трапеция (по
определению), тогда
SABMN=(NM+AB)/2*ED. Подставляем ранее выявленные равенства, получаем:
SABMN=(NM+2NM)/2*CE=3NM/2*CE=1,5NM*CE=1,5*16=24
Ответ: SABMN=24
Поделитесь решением
Присоединяйтесь к нам...
В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
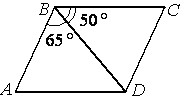Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
65° и 50°. Найдите меньший угол параллелограмма.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.
В трапецию, сумма длин боковых сторон которой равна 16, вписана окружность. Найдите длину средней линии трапеции.
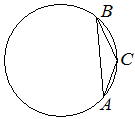В треугольнике ABC угол C равен 135°, AB=14√2. Найдите радиус окружности, описанной около этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: