
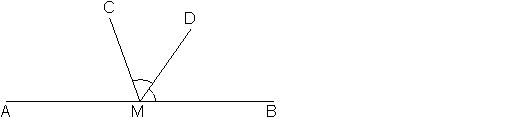
 На прямой AB взята точка M. Луч MD – биссектриса угла CMB. Известно, что /DMC=60°. Найдите угол CMA. Ответ дайте в градусах.
На прямой AB взята точка M. Луч MD – биссектриса угла CMB. Известно, что /DMC=60°. Найдите угол CMA. Ответ дайте в градусах.
Так как MD -
биссектриса, то /DMC=/DMB=60°.
Развернутый угол AMB=180° (по определению).
Тогда 180°=/CMA+/DMC+/DMB
180°=/CMA+60°+60°
/CMA=180°-60°-60°
/CMA=60°
Ответ: /CMA=60°
Поделитесь решением
Присоединяйтесь к нам...
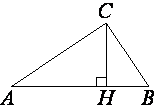 В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√
В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=7.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=7.
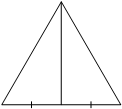 Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.
 Основания трапеции равны 11 и 19, а высота равна 9. Найдите среднюю линию этой трапеции.
Основания трапеции равны 11 и 19, а высота равна 9. Найдите среднюю линию этой трапеции.
Комментарии: