Высота BH ромба ABCD делит его сторону AD на отрезки AH=4 и HD=1. Найдите площадь ромба.
Площадь
ромба равна S=ah, где a - сторона ромба, h - высота ромба.
AD=AH+HD=4+1=5.
AD=AB=BC=CD (по
определению ромба).
Рассмотрим треугольник ABH.
ABH -
прямоугольный (т.к. BH -
высота), тогда по
теореме Пифагора: AB2=BH2+AH2
52=BH2+42
25=BH2+16
BH2=9
BH=3
Sромба=AD*BH=5*3=15
Ответ: Sромба=15
Поделитесь решением
Присоединяйтесь к нам...
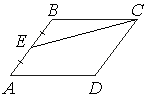Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 5 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Найдите площадь треугольника, изображённого на рисунке.
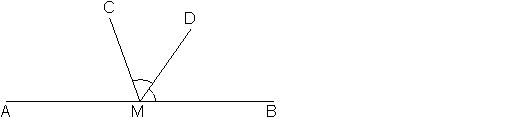На прямой AB взята точка M. Луч MD – биссектриса угла CMB. Известно, что /DMC=60°. Найдите угол CMA. Ответ дайте в градусах.
Площадь равнобедренного треугольника равна 1600√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-05-29 21:26:43) Администратор: Сабин, главное, что Вы сами все поняли, без подсказки.
(2014-05-29 21:14:17) Сабит: извините,это я не прав,я забыль,что ромб имеет все свойства квадрата,а у квадрата все стороны равны.
(2014-05-29 21:11:24) Сабит: Вы в формулу Пифагора подставили место AB в квадрате 5 в квадрате,а там сказано,что AD=5,а не AB.