
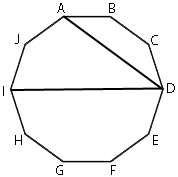
 ABCDEFGHIJ – правильный десятиугольник. Найдите угол ADI. Ответ дайте в градусах.
ABCDEFGHIJ – правильный десятиугольник. Найдите угол ADI. Ответ дайте в градусах.
Вариант 1 (Предложил пользователь Светлана)
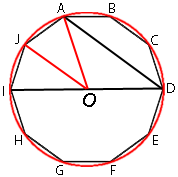 Вокруг любого
правильного многоугольника можно описать окружность, сделаем это.
Вокруг любого
правильного многоугольника можно описать окружность, сделаем это.
Очевидно, что отрезки, проведенные из центра окружности к углам девятиугольника образуют равные углы, так как разбивают девятиугольник на равные треугольники.
Такой угол (например ∠AOJ) равен 360°/10=36°
Тогда ∠AOI равен:
∠AOI=36°*2=72°
∠AOI является
центральным, следовательно градусная мера дуги IJA тоже равна 76°
∠ADI тоже опирается на эту же дугу, но является
вписанным, следовательно:
∠ADI=72°/2=36° (по
теореме о вписанном угле)
Ответ: 36
 Проведем отрезки AC и BD.
Проведем отрезки AC и BD.Поделитесь решением
Присоединяйтесь к нам...
 В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 4. Найдите площадь трапеции.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 4. Найдите площадь трапеции.
 Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
 Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
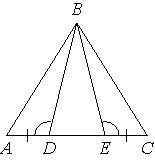 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
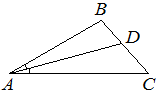 В треугольнике ABC известно, что ∠BAC=28°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
В треугольнике ABC известно, что ∠BAC=28°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Комментарии: