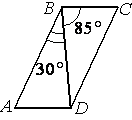Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 85° и 30°. Найдите меньший угол параллелограмма.
По
свойству
параллелограмма /B=/D=85°+30°=115° и /A=/C.
Найдем углы A и C.
Стороны AD и BC параллельны (по
определению параллелограмма). Если рассмотреть BD как секущую к этим параллельным прямым, то становится очевидным, что /CBD=/ADB=85° (т.к. они
накрест лежащие).
Рассмотрим треугольник ABD.
По
теореме о сумме углов треугольника мы можем написать: 180°=/ABD+/BDA+/A
180°=30°+85°+/A
/A=65°=/C
115>65, следовательно углы A и C - меньшие.
Ответ: меньший угол равен 65°.
Поделитесь решением
Присоединяйтесь к нам...
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
В треугольнике ABC известно, что AB=8, BC=10, AC=14. Найдите cos∠ABC.
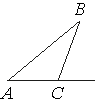В треугольнике ABC угол C равен 133°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Длина хорды окружности равна 60, а расстояние от центра окружности до этой хорды равно 40. Найдите диаметр окружности.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-03-05 20:33:00) Администратор: Сэм, уточните, где именно ошибка?
(2016-03-04 17:36:26) сэм: у вас ошибка в написание