
 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 25°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 25°. Найдите больший угол параллелограмма.
По
свойству
параллелограмма /A=/C=25°+45°=70° и /B=/D.
Найдем углы B и D.
Стороны AD и BC параллельны (по
определению параллелограмма). Если рассмотреть AC как секущую к этим параллельным прямым, то становится очевидным, что /DAC=/BCA=45° (т.к. они
накрест лежащие).
Рассмотрим треугольник ABC.
По
теореме о сумме углов треугольника мы можем написать: 180°=/CAB+/B+/BCA
180°=25°+/B+45°
/B=110°=/D
110>70, следовательно углы B и D - бОльшие.
Ответ: больший угол равен 110°.
Поделитесь решением
Присоединяйтесь к нам...
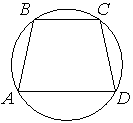 Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
 Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
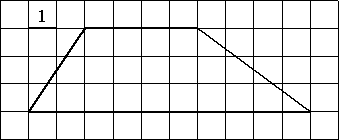 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
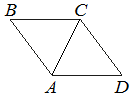 В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
Синус острого угла A треугольника ABC равен 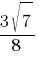 . Найдите CosA.
. Найдите CosA.
Комментарии: