
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
 Рассмотрим рисунок. Проведем отрезок MP, как показано на рисунке. BM - диаметр малой окружности (по условию задачи), следовательно треугольник BMP -
прямоугольный с гипотенузой BM (по
свойству описанной окружности).
Рассмотрим рисунок. Проведем отрезок MP, как показано на рисунке. BM - диаметр малой окружности (по условию задачи), следовательно треугольник BMP -
прямоугольный с гипотенузой BM (по
свойству описанной окружности).
Рассмотрим треугольники BMP и CPM:
MP - общая сторона
BP=PC (по условию задачи)
/BPM=/CPM, т.к. /BPM - прямой, а /CPM - ему
смежный.
Следовательно треугольники BMP и CPM равны (по
первому признаку). Отсюда следует, что BM=MC=MA.
Рассмотрим треугольник BMC. Т.к. MB=MC, то этот треугольник
равнобедренный, следовательно /MCP=/PBM (по
свойству равнобедренных треугольников).
В треугольнике ABM аналогичная ситуация, /BAM=/ABM.
Т.е. получается, что /BAM+/MCP=/ABC. Из
теоремы о сумме углов треугольника следует, 180°=/BAM+/MCP+/ABC
180°=/ABC+/ABC
180°=2*/ABC
90°=/ABC
Из чего следует, что треугольник ABC -
прямоугольный. По
свойству описанной окружности следует, что точка М - центр окружности, следовательно AC - диаметр => AC=2*R=2*7=14.
Ответ: AC=14.
Поделитесь решением
Присоединяйтесь к нам...
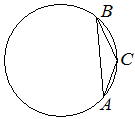 В треугольнике ABC угол C равен 135°, AB=14√2. Найдите радиус окружности, описанной около этого треугольника.
В треугольнике ABC угол C равен 135°, AB=14√2. Найдите радиус окружности, описанной около этого треугольника.
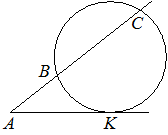 Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=4, BC=32. Найдите AK.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=4, BC=32. Найдите AK.
Какое из следующих утверждений верно?
1) Площадь квадрата равна произведению двух его смежных сторон.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
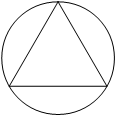 Радиус окружности, описанной около равностороннего треугольника, равен 2√
Радиус окружности, описанной около равностороннего треугольника, равен 2√
 В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
Комментарии: